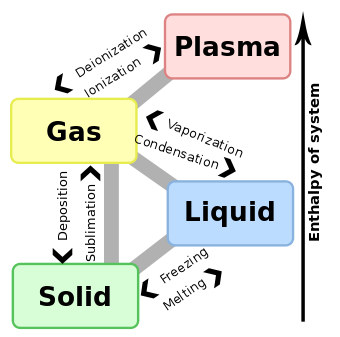
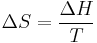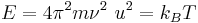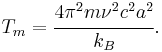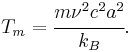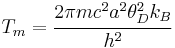Melting point
The melting point of a solid is the temperature at which the vapor pressure of the solid and the liquid are equal. At the melting point the solid and liquid phase exist in equilibrium. When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing point or crystallization point. Because of the ability of some substances to supercool, the freezing point is not considered to be a characteristic property of a substance. When the "characteristic freezing point" of a substance is determined, in fact the actual methodology is almost always "the principle of observing the disappearance rather than the formation of ice", that is, the melting point.[1]
Contents |
Fundamentals

For most substances, melting and freezing points are approximately equal. For example, the melting point and freezing point of the element mercury is 234.32 kelvin (−38.83 °C or −37.89 °F). However, certain substances possess differing solid-liquid transition temperatures. For example, agar melts at 85 °C (185 °F) and solidifies from 31 °C to 40 °C (89.6 °F to 104 °F); this process is known as hysteresis.
Certain materials, such as glass, may harden without crystallizing; these are called amorphous solids. Amorphous materials as well as some polymers do not have a true melting point as there is no abrupt phase change at any specific temperature. Instead, there is a gradual change in their viscoelastic properties over a range of temperatures. Such materials are characterized by a glass transition which occurs at a glass transition temperature which may be roughly defined as the "knee" point of the material's density vs. temperature graph.
The melting point of ice at 1 atmosphere of pressure is very close [2] to 0 °C (32 °F, 273.15 K), this is also known as the ice point. In the presence of nucleating substances the freezing point of water is the same as the melting point, but in the absence of nucleators water can supercool to −42 °C (−43.6 °F, 231 K) before freezing.
Unlike the boiling point, the melting point is relatively insensitive to pressure because the solid/liquid transition represents only a small change in volume.[3][4] Melting points are often used to characterize organic and inorganic compounds and to ascertain their purity. The melting point of a pure substance is always higher and has a smaller range than the melting point of an impure substance. The more impurity is present, the lower the melting point and the broader the range. Eventually, a minimum melting point will be reached. The mixing ratio that results in the lowest possible melting point is known as the eutectic point.
The chemical element with the highest melting point is tungsten, at 3683 K (3410 °C, 6170 °F) making it excellent for use as filaments in light bulbs. The often-cited carbon does not melt at ambient pressure but sublimes at about 4000 K; a liquid phase only exists above pressures of 10 MPa and estimated 4300–4700 K. Tantalum hafnium carbide (Ta4HfC5) is a refractory compound with a very high melting point of 4488 K (4215 °C, 7619 °F).[5] At the other end of the scale, helium does not freeze at all at normal pressure, even at temperatures very close to absolute zero; pressures over 20 times normal atmospheric pressure are necessary.
Melting point measurements
Many laboratory techniques exist for the determination of melting points. A Kofler bench is a metal strip with a temperature gradient (range room temperature to 300 °C). Any substance can be placed on a section of the strip revealing its thermal behaviour at the temperature at that point. Differential scanning calorimetry gives information on melting point together with its enthalpy of fusion.
A basic melting point apparatus for the analysis of crystalline solids consists of a oil bath with a transparent window (most basic design: a Thiele tube) and a simple magnifier. The several grains of a solid are placed in a thin glass tube and partially immersed in the oil bath. The oil bath is heated (and stirred) and with the aid of the magnifier (and external light source) melting of the individual crystals at a certain temperature can be observed. In large/small devices, the sample is placed in a heating block, and optical detection is automated.
Thermodynamics

Not only is heat required to raise the temperature of the solid to the melting point, but the melting itself requires heat called the heat of fusion.
From a thermodynamics point of view, at the melting point the change in Gibbs free energy (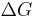 ) of the material is zero, but the enthalpy (
) of the material is zero, but the enthalpy ( ) and the entropy (
) and the entropy ( ) of the material are increasing (
) of the material are increasing (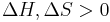 ). Melting phenomenon happens when the Gibbs free energy of the liquid becomes lower than the solid for that material. At various pressures this happens at a specific temperature. It can also be shown that:
). Melting phenomenon happens when the Gibbs free energy of the liquid becomes lower than the solid for that material. At various pressures this happens at a specific temperature. It can also be shown that:
The " ","
","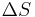 ", and "
", and "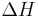 " in the above are respectively the temperature at the melting point, change of entropy of melting, and the change of enthalpy of melting.
" in the above are respectively the temperature at the melting point, change of entropy of melting, and the change of enthalpy of melting.
Carnelley’s Rule
In organic chemistry Carnelley’s Rule, established in 1882 by Thomas Carnelley, stated that high molecular symmetry is associated with high melting point.[6] Carnelley based his rule on examination of 15,000 chemical compounds. For example for three structural isomers with molecular formula C5H12 the melting point increases in the series isopentane −160 °C (113 K) n-pentane −129.8 °C (143 K) and neopentane −18 °C (255 K). Likewise in xylenes and also dichlorobenzenes the melting point increases in the order meta, ortho and then para. Pyridine has a lower symmetry than benzene hence its lower melting point but the melting point again increases with diazine and triazines. Many cage-like compounds like adamantane and cubane with high symmetry have very high melting points.
A high melting point results from a high heat of fusion, a low entropy of fusion, or a combination of both. In highly symmetrical molecules the crystal phase is densely packed with many efficient intermolecular interactions resulting in a higher enthalpy change on melting.
Predicting the melting point of substances
An attempt to predict the bulk melting point of crystalline materials was first made in 1910 by Lindemann[7]. The idea behind the theory was the observation that the average amplitude of thermal vibrations increase with increasing temperature. Melting initiates when the amplitude of vibration becomes large enough for adjacent atoms to partly occupy the same space. The Lindemann criterion states that melting is expected when the root mean square vibration amplitude exceeds a threshold value.
If we assume that all atoms in a crystal vibrate with the same frequency  , the average thermal energy can be estimated using the equipartition theorem to be[8]
, the average thermal energy can be estimated using the equipartition theorem to be[8]
where  is the atomic mass,
is the atomic mass,  is the frequency,
is the frequency,  is the average vibration amplitude,
is the average vibration amplitude, 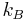 is the Boltzmann constant, and
is the Boltzmann constant, and  is the absolute temperature. If the threshold value of
is the absolute temperature. If the threshold value of 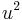 is
is 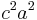 where
where  is the Lindemann constant and
is the Lindemann constant and 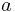 is the atomic spacing, the melting point is estimated as
is the atomic spacing, the melting point is estimated as
Several other expressions for the estimated melting temperature can be obtained depending on the estimate of the average thermal energy[9]. Another commonly used expression for the Lindemann criterion is[10]
If we use the expression for the Debye frequency for  , we have
, we have
where 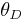 is the Debye temperature and
is the Debye temperature and 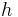 is the Planck constant. Values of
is the Planck constant. Values of  range from 0.15-0.3 for most materials[11].
range from 0.15-0.3 for most materials[11].
Melting point of radioactive materials
The characterization of highly radioactive materials is an important part of the overall optimization strategy for storage and treatment processes. An important parameter for this optimization is the crystallization temperature of liquid wastes. The measurement of crystallization temperatures of these materials is a challenging task and has been solved by the development and deployment of a bespoke imaging system.
The design philosophy of this instrument will be discussed, the approach taken described and the unique problems encountered during development highlighted. In outline, the instrument consists of:
- A computer controlled unit that allows highly reproducible heating and cooling of a sample. This unit is contained in a heavily shielded facility
- A vision system that images the sample remotely through the shield window.
- Storage and analysis of the subsequent images.
Results obtained for model solutions will be described and examples from the preliminary studies of highly radioactive solutions given.
See also
- Degree of frost
- Freezing-point depression
- List of elements by melting point
- Phases of matter
- Triple point
- Vicat softening point - the determination of the softening point for materials that have no definite melting point.
- Liquidus temperature
- Slip melting point
- Solidus temperature
References
- ↑ Ramsay, J. A. (1949). "A new method of freezing-point determination for small quantities". J. Exp. Biol. 26 (1): 57–64. PMID 15406812. http://jeb.biologists.org/cgi/reprint/26/1/57.pdf.
- ↑ The melting point of purified water has been measured to be 0.002519 +/- 0.000002 degrees Celsius - see R. Feistel and W. Wagner (2006). "A New Equation of State for H2O Ice Ih". J. Phys. Chem. Ref. Data 35: 1021–1047. doi:10.1063/1.2183324.
- ↑ The exact relationship is expressed in the Clausius-Clapeyron relation.
- ↑ "J10 Heat: Change of aggregate state of substances through change of heat content: Change of aggregate state of substances and the equation of Clapeyron-Clausius". http://mpec.sc.mahidol.ac.th/RADOK/physmath/PHYSICS/j10.htm. Retrieved 2008-02-19.
- ↑ hafnium entry at Britannica.com
- ↑ Brown, R. J. C. & R. F. C. (June 2000). "Melting Point and Molecular Symmetry". Journal of Chemical Education 77 (6): 724. doi:10.1021/ed077p724.
- ↑ Lindemann FA (1910). "The calculation of molecular vibration frequencies". Physik. Z. 11: 609–612.
- ↑ Sorkin, S., (2003), Point defects, lattice structure, and melting, Thesis, Technion, Israel.
- ↑ Solyom, J., (2007), Fundamentals of the physics of solids, Volume 2, Springer.
- ↑ Hofmann, P., (2008), Solid state physics: an introduction, Wiley-VCH.
- ↑ Nelson, D. R., (2002), Defects and geometry in condensed matter physics, Cambridge University Press.
External links
- Melting and boiling point tables vol. 1 by Thomas Carnelley (Harrison, London, 1885-1887)
- Melting and boiling point tables vol. 2 by Thomas Carnelley (Harrison, London, 1885-1887)
|
|||||||||||||||||||||||||